Skip to content
Search

Zig NEWS

Cover image for Fast, multi-platform, SIMD math library in Zig
Michal Ziulek
Michal Ziulek

Posted on • Updated on

Fast, multi-platform, SIMD math library in Zig

#math #simd #gamedev #library

GitHub homepage: zmath

Introduction

Zig programming language does not support operator overloading - instead, it provides builtin Vector types.

const F32x4 = @Vector(4, f32);

const v0 = F32x4{ 1.0, 2.0, 3.0, 4.0 };
const v1 = F32x4{ 1.0, 2.0, 3.0, 4.0 };

const v = v0 + v1;
Enter fullscreen mode Exit fullscreen mode

When compiled to x86_64 with zig build -Dcpu=x86_64 -Drelease-fast=true above code will map to a single SIMD instruction:

addps xmm0, xmm1
Enter fullscreen mode Exit fullscreen mode

This is very nice because we get fast SIMD code without using CPU specific intrinsics - when compiled for ARM architecture we would get single NEON instruction. Furthermore, when we extend our code to:

const F32x8 = @Vector(8, f32);

const v0 = F32x8{ 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0 };
const v1 = F32x8{ 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0 };

const v = v0 + v1;
Enter fullscreen mode Exit fullscreen mode

and compile with zig build -Dcpu=x86_64 -Drelease-fast=true we get:

addps xmm0, xmm2
addps xmm1, xmm3
Enter fullscreen mode Exit fullscreen mode

So, we have extended our vector width from 4 to 8 and our code is still very efficient. Target architecture does not natively support vector width 8 so compiler generated 2 x SIMDx4 code.

When we compile above code with zig build -Dcpu=x86_64+avx -Drelease-fast=true we get:

vaddps ymm0, ymm0, ymm1
Enter fullscreen mode Exit fullscreen mode

AVX extension adds native support for vector width 8 and compiler takes advantage of this fact generating only single instruction. Of course Zig supports all fundamental operators, not only '+'.

Above concepts are very powerful because they allow us to write generic SIMD code that will compile to multiple vector widths and multiple CPU architectures.

Example 1 - zmath.sin()

Consider code below. It computes sin() over large array using zmath lib. When you work with vector width 8 - compiler generates SIMDx8 code. When you increase vector width to 16 - compiler generates 2 x SIMDx8 code.

const zm = @import("zmath.zig");

const SimdType = zm.F32x16;
// const SimdType = zm.F32x8;

fn processData(data: []f32, num_elements: u32) void {
    var i: u32 = 0;
    while (i < num_elements) : (i += zm.veclen(SimdType)) {
        var v = zm.load(data[i..], SimdType, 0);
        v = zm.sin(v);
        zm.store(data[i..], v, 0);
    }
}
Enter fullscreen mode Exit fullscreen mode

In this case 2 x SIMDx8 code achieves 0.98 uOps/cycle. SIMDx8 code achieves only 0.32 uOps/cycle. This is because 2 x SIMDx8 code generates more independent uOps per iteration and HW resources are better utilized - more uOps are executed in parallel.

;
; SimdType = F32x8
; zmath.sin(v: SimdType)
; SIMDx8 code (-Dcpu=x86_64+avx+fma)
; 0.32 uOps/cycle according to llvm-mca
;
vmovap      ymm1, ymm0
vmulps      ymm0, ymm0, ymmword ptr [rip + .LCPI0_0]
vroundps    ymm0, ymm0, 0
vmulps      ymm0, ymm0, ymmword ptr [rip + .LCPI0_1]
vaddps      ymm0, ymm1, ymm0
vandps      ymm1, ymm0, ymmword ptr [rip + .LCPI0_2]
vorps       ymm1, ymm1, ymmword ptr [rip + .LCPI0_3]
vandps      ymm2, ymm0, ymmword ptr [rip + .LCPI0_4]
vsubps      ymm1, ymm1, ymm0
vcmpleps    ymm2, ymm2, ymmword ptr [rip + .LCPI0_5]
vblendvps   ymm0, ymm1, ymm0, ymm2
vmulps      ymm1, ymm0, ymm0
vmovaps     ymm2, ymmword ptr [rip + .LCPI0_6]
vfmadd213ps ymm2, ymm1, ymmword ptr [rip + .LCPI0_7]
vfmadd213ps ymm2, ymm1, ymmword ptr [rip + .LCPI0_8]
vfmadd213ps ymm2, ymm1, ymmword ptr [rip + .LCPI0_9]
vfmadd213ps ymm2, ymm1, ymmword ptr [rip + .LCPI0_10]
vfmadd213ps ymm2, ymm1, ymmword ptr [rip + .LCPI0_11]
vmulps      ymm0, ymm0, ymm2
Enter fullscreen mode Exit fullscreen mode 
;
; SimdType = F32x16
; zmath.sin(v: SimdType)
; 2 x SIMDx8 code (-Dcpu=x86_64+avx+fma)
; 0.98 uOps/cycle according to llvm-mca
;
vmovaps     ymm2, ymm1
vmovaps     ymm3, ymm0
vmovaps     ymm0, ymmword ptr [rip + .LCPI0_0]
vmulps      ymm1, ymm1, ymm0
vmulps      ymm0, ymm3, ymm0
vroundps    ymm0, ymm0, 0
vroundps    ymm1, ymm1, 0
vmovaps     ymm4, ymmword ptr [rip + .LCPI0_1]
vmulps      ymm0, ymm0, ymm4
vmulps      ymm1, ymm1, ymm4
vaddps      ymm1, ymm2, ymm1
vaddps      ymm0, ymm3, ymm0
vmovaps     ymm2, ymmword ptr [rip + .LCPI0_2]
vandps      ymm3, ymm0, ymm2
vandps      ymm2, ymm1, ymm2
vmovaps     ymm4, ymmword ptr [rip + .LCPI0_3]
vorps       ymm2, ymm2, ymm4
vorps       ymm3, ymm3, ymm4
vmovaps     ymm4, ymmword ptr [rip + .LCPI0_4]
vandps      ymm5, ymm1, ymm4
vandps      ymm4, ymm0, ymm4
vsubps      ymm3, ymm3, ymm0
vsubps      ymm2, ymm2, ymm1
vmovaps     ymm6, ymmword ptr [rip + .LCPI0_5]
vcmpleps    ymm4, ymm4, ymm6
vcmpleps    ymm5, ymm5, ymm6
vblendvps   ymm1, ymm2, ymm1, ymm5
vblendvps   ymm0, ymm3, ymm0, ymm4
vmulps      ymm2, ymm0, ymm0
vmulps      ymm3, ymm1, ymm1
vmovaps     ymm4, ymmword ptr [rip + .LCPI0_6]
vmovaps     ymm5, ymmword ptr [rip + .LCPI0_7]
vmovaps     ymm6, ymm5
vfmadd213ps ymm6, ymm3, ymm4
vfmadd213ps ymm5, ymm2, ymm4
vmovaps     ymm4, ymmword ptr [rip + .LCPI0_8]
vfmadd213ps ymm5, ymm2, ymm4
vfmadd213ps ymm6, ymm3, ymm4
vmovaps     ymm4, ymmword ptr [rip + .LCPI0_9]
vfmadd213ps ymm6, ymm3, ymm4
vfmadd213ps ymm5, ymm2, ymm4
vmovaps     ymm4, ymmword ptr [rip + .LCPI0_10]
vfmadd213ps ymm5, ymm2, ymm4
vfmadd213ps ymm6, ymm3, ymm4
vmovaps     ymm4, ymmword ptr [rip + .LCPI0_11]
vfmadd213ps ymm6, ymm3, ymm4
vfmadd213ps ymm5, ymm2, ymm4
vmulps      ymm0, ymm0, ymm5
vmulps      ymm1, ymm1, ymm6
Enter fullscreen mode Exit fullscreen mode

Notice how easy it is to change the vector width - you only need to change the SimdType constant - rest of the code stays unchanged. This is great because we can experiment with different vector widths for a given algorithm and choose the fastest one.

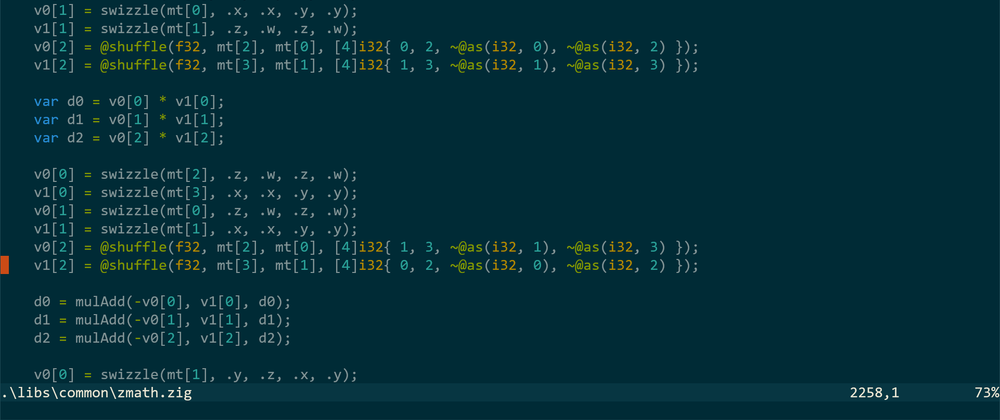
Example 2 - zmath.mul(Mat, Mat)

4x4 matrix multiplication is very common in 3D game development. zmath has very simple and efficient implementation:

var result: Mat = undefined;
comptime var row: u32 = 0;
inline while (row < 4) : (row += 1) {

var vx = @shuffle(f32, m0[row], undefined, [4]i32{ 0, 0, 0, 0 });
var vy = @shuffle(f32, m0[row], undefined, [4]i32{ 1, 1, 1, 1 });
var vz = @shuffle(f32, m0[row], undefined, [4]i32{ 2, 2, 2, 2 });
var vw = @shuffle(f32, m0[row], undefined, [4]i32{ 3, 3, 3, 3 });

vx = vx * m1[0];
vy = vy * m1[1];
vz = vz * m1[2];
vw = vw * m1[3];
vx = vx + vz;
vy = vy + vw;
vx = vx + vy;
result[row] = vx;
}
Enter fullscreen mode Exit fullscreen mode

When compiled with: zig build -Dcpu=x86_64+avx+fma -Drelease-fast=true we get fast assembly shown below. Theoretical characteristic (llvm-mca) of this code on Zen2 is:

Dispatch Width: 4
uOps Per Cycle: 3.30
IPC: 3.30
Block RThroughput: 12.3

vmovups      xmm1, xmmword ptr [rdx]
vmovups      xmm2, xmmword ptr [rdx + 16]
vmovups      xmm3, xmmword ptr [rdx + 32]
vmovups      xmm0, xmmword ptr [rdx + 48]
vbroadcastss xmm4, dword ptr [rsi]
vbroadcastss xmm5, dword ptr [rsi + 4]
vbroadcastss xmm6, dword ptr [rsi + 8]
vbroadcastss xmm7, dword ptr [rsi + 12]
vmulps       xmm4, xmm4, xmm1
vmulps       xmm5, xmm5, xmm2
vmulps       xmm6, xmm6, xmm3
vaddps       xmm4, xmm4, xmm6
vmulps       xmm6, xmm7, xmm0
vaddps       xmm5, xmm5, xmm6
vaddps       xmm8, xmm4, xmm5
vbroadcastss xmm5, dword ptr [rsi + 16]
vbroadcastss xmm6, dword ptr [rsi + 20]
vbroadcastss xmm7, dword ptr [rsi + 24]
vbroadcastss xmm4, dword ptr [rsi + 28]
vmulps       xmm5, xmm5, xmm1
vmulps       xmm6, xmm6, xmm2
vmulps       xmm7, xmm7, xmm3
vaddps       xmm5, xmm5, xmm7
vmulps       xmm4, xmm4, xmm0
vaddps       xmm4, xmm6, xmm4
vaddps       xmm9, xmm5, xmm4
vbroadcastss xmm5, dword ptr [rsi + 32]
vbroadcastss xmm6, dword ptr [rsi + 36]
vbroadcastss xmm7, dword ptr [rsi + 40]
vbroadcastss xmm4, dword ptr [rsi + 44]
vmulps       xmm5, xmm5, xmm1
vmulps       xmm6, xmm6, xmm2
vmulps       xmm7, xmm7, xmm3
vaddps       xmm5, xmm5, xmm7
vmulps       xmm4, xmm4, xmm0
vaddps       xmm4, xmm6, xmm4
vaddps       xmm10, xmm5, xmm4
vbroadcastss xmm5, dword ptr [rsi + 48]
vbroadcastss xmm6, dword ptr [rsi + 52]
vbroadcastss xmm7, dword ptr [rsi + 56]
vbroadcastss xmm4, dword ptr [rsi + 60]
vmulps       xmm1, xmm5, xmm1
vmulps       xmm2, xmm6, xmm2
vmulps       xmm3, xmm7, xmm3
vaddps       xmm1, xmm1, xmm3
vmulps       xmm0, xmm4, xmm0
vaddps       xmm0, xmm2, xmm0
vaddps       xmm0, xmm1, xmm0
Enter fullscreen mode Exit fullscreen mode

Example 3 - zmath.round()

round() is very useful operation - zmath.sin() uses it to perform input value reduction into [-pi; pi) range. zmath uses inline assembly on x86_64 to make it as fast as possible. As you can see below, x86_64 SSE and ARM NEON paths are implemented as generic Zig code ('else' block). x86_64 AVX+ paths are optimized and map to a single instruction.

pub fn round(v: anytype) @TypeOf(v) {
    const T = @TypeOf(v);
    if (cpu_arch == .x86_64 and has_avx) {
        if (T == F32x4) {
            return asm ("vroundps $0, %%xmm0, %%xmm0"
                : [ret] "={xmm0}" (-> T),
                : [v] "{xmm0}" (v),
            );
        } else if (T == F32x8) {
            return asm ("vroundps $0, %%ymm0, %%ymm0"
                : [ret] "={ymm0}" (-> T),
                : [v] "{ymm0}" (v),
            );
        } else if (T == F32x16 and has_avx512f) {
            return asm ("vrndscaleps $0, %%zmm0, %%zmm0"
                : [ret] "={zmm0}" (-> T),
                : [v] "{zmm0}" (v),
            );
        } else if (T == F32x16 and !has_avx512f) {
            const arr: [16]f32 = v;
            var ymm0 = @as(F32x8, arr[0..8].*);
            var ymm1 = @as(F32x8, arr[8..16].*);
            ymm0 = asm ("vroundps $0, %%ymm0, %%ymm0"
                : [ret] "={ymm0}" (-> F32x8),
                : [v] "{ymm0}" (ymm0),
            );
            ymm1 = asm ("vroundps $0, %%ymm1, %%ymm1"
                : [ret] "={ymm1}" (-> F32x8),
                : [v] "{ymm1}" (ymm1),
            );
            return @shuffle(
                f32, ymm0, ymm1,
                [16]i32{
                    0, 1, 2, 3, 4, 5, 6, 7,
                    -1, -2, -3, -4, -5, -6, -7, -8
                }
            );
        }
    } else {
        const sign = andInt(v, splatNegativeZero(T));
        const magic = orInt(splatNoFraction(T), sign);
        var r1 = v + magic;
        r1 = r1 - magic;
        const r2 = abs(v);
        const mask = r2 <= splatNoFraction(T);
        return select(mask, r1, v);
    }
}
Enter fullscreen mode Exit fullscreen mode

Library overview

zmath library builds on top of Zig provided features and adds higher level functionality useful for game developers. Few fundamental types are provided F32x4, F32x8, F32x16, Boolx4, Boolx8 and Boolx16. List of all provided functions can be found here. I have investigated assembly code for each function and when compiler generated version wasn't efficient I have provided faster inline assembly for x86_64 architecture.

Functions are divided into several classes:

Initialization functions 

const zm = @import("zmath.zig");

const v4 = zm.f32x4(1.0, 2.0, 3.0, 4.0);
const v8 = zm.f32x8(1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0);

// set all components to a single value
const v16 = zm.f32x16s(math.pi * 0.25);

const v = v4 * v4;
const b = v > v4; // b is a Boolx4 vector
if (zm.all(b, 0)) { // if all components are 'true'
  // do something
}

// load 3 components from memory, 4th component will be set to 0
var vv4 = zm.load(mem[0..], F32x4, 3);

// load 2 components from memory and put them into F32x8
var vv8 = zm.load(mem[32..], F32x8, 2);

// load 7 components from memory and put them into F32x16
var vv16 = zm.load(mem[64..], F32x16, 7); 

// process data...
vv4 = zm.sin(vv4);
vv8 = zm.saturate(vv8);
vv16 = zm.cos(vv16);

zm.store(mem[0..], vv4, 3); // store 3 components
zm.store(mem[32..], vv8, 8); // store 8 components

// store all vector components (16 in this case)
zm.store(mem[64..], vv16, 0);
Enter fullscreen mode Exit fullscreen mode

Functions that work on all vector components 

const zm = @import("zmath.zig");

const v4 = zm.sin(zm.f32x4(1.0, 2.0, 3.0, 4.0));
const v8 = zm.sin(zm.f32x8(1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0));
const v16 = zm.sin(zm.f32x16s(math.pi * 0.25));
Enter fullscreen mode Exit fullscreen mode

When compiled with zig build -Dcpu=x86_64 -Drelease-fast=true we get efficient SIMDx4 assembly for the first invocation, 2 x SIMDx4 assembly for the second invocation and 4 x SIMDx4 for the third one. When we compile for AVX capable CPUs we get SIMDx4 code for the first invocation, SIMDx8 for the second one and 2 x SIMDx8 for the last one.

2D, 3D, 4D vector functions

pub const Vec = F32x4;

Those functions treat F32x4 type as 2D, 3D or 4D vector. Number in the function name suffix tells us how many components are used. For example, dot2 performs dot product operation treating vectors as 2D, cross3 function uses x, y, z components to perform cross product operation and so on.

Vector arithmetic is expressed naturally, for example:

const vr0 = v0 + v1 - v2;
const scalar: f32 = 2.0;
const vr1 = v0 + zm.f32x4s(scalar) * zm.f32x4(1.0, 2.0, 3.0, 4.0);

// zm.dotN() returns scalar replicated on all vector components
const vr2 = zm.dot3(v0, v1) / v3;
Enter fullscreen mode Exit fullscreen mode

Vector comparison is accomplished with builtin operators and zmath.all(), zmath.any() functions.

if (zm.all(v0 > v1, 3)) { // if all first 3 components are 'true'
    // do something
}

if (zm.any(v0 > v1, 3)) { // if any of the first 3 components is 'true'
    // do something
}
Enter fullscreen mode Exit fullscreen mode

Matrix functions

pub const Mat = [4]F32x4;

All typical matrix operations are available. There are several overloads of zmath.mul() function:

const zm = @import("zmath.zig");
zm.mul(zm.Vec, zm.Mat) // Vec treated as a row vector
zm.mul(zm.Mat, zm.Vec) // Vec treated as a column vector
zm.mul(f32, zm.Mat)
zm.mul(zm.Mat, f32)
zm.mul(zm.Quat, zm.Quat)
zm.mul(zm.Vec, f32)
zm.mul(f32, zm.Vec)
Enter fullscreen mode Exit fullscreen mode

Some examples:

const speed = zm.f32x4s(10.0);
const delta_time = zm.f32x4s(demo.frame_stats.delta_time);

const transform = zm.mul(
    zm.rotationX(demo.camera.pitch),
    zm.rotationY(demo.camera.yaw),
);
var forward = zm.normalize3(
    zm.mul(zm.f32x4(0.0, 0.0, 1.0, 0.0), transform),
);

zm.store(demo.camera.forward[0..], forward, 3);

const right = speed * delta_time * zm.normalize3(
    zm.cross3(
        zm.f32x4(0.0, 1.0, 0.0, 0.0),
        forward,
    )
);
forward = speed * delta_time * forward;
Enter fullscreen mode Exit fullscreen mode

Quaternion functions

pub const Quat = F32x4;

All typical quaternion operations are available. Some examples:

const q0 = zm.quatFromMat(m0);
const q1 = zm.quatFromMat(m1);
const qp = zm.mul(q0, q1);

const q = zm.slerp(q0, q1, 0.5);

const m = zm.quatToMat(q);
Enter fullscreen mode Exit fullscreen mode

Summary

Thanks for reading! If you like this article please visit zig-gamedev project - recently I have released several 'intro applications' which show step by step how to use zmath lib and graphics lib - you can find them here.

Top comments (6)

Collapse
 
yanwenjiepy profile image
花大喵 •

Great to enrich the library of zig math

Collapse
 
austinclem1 profile image
Austin Clements •

This is awesome!! For releasing software using SIMD would your approach be to release multiple builds with different processor extensions enabled? Alternatively is there a way to have one binary that determines SIMD capabilities at runtime?

Collapse
 
nic0nic0ni profile image
Kan Liu •

In example 2, the code was compiled with fma, why didn't the assembly show vfmaddps?

Collapse
 
tpfaff100 profile image
Thomas Poff •

Hi. Nice stuff, really.
I can get a lot to work but on the zm.sin() calls I get...

~/zig/zmathproj % zig build-exe -Dcpu=x86_64 -Drelease-fast=true test.zig
test.zig:40:15: error: root struct of file 'libs.zmath.build' has no member named 'sin'
const zz = zm.sin(zm.f32x16(1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0));

Yeah I'm on a mac using zig 0.11.0 have gotten the library included and can call into it.

I can switch to Linux if need be just was thinking this should work since many other profiles I've tried have been ok.

I have no problems, for instance with-
const v0 = F32x4{ 1.0, 2.0, 3.0, 4.0 };
const v1 = F32x4{ 1.0, 2.0, 3.0, 4.0 };
const v2 = v0 + v1;
....
std.debug.print("{} \n", .{v2});

Works great. Any ideas why the trig functions are not a go? Thank you.
Getting this to work would be a boon to my laser imaging system, which in the past has was mostly an analog, quadrature burr-brown oscillator chips. I also used a digital system with six channels of D/A + now would like to convert over to digital, finally, since everything can be done digitally "kind of" in real time now (with big canned matrices of values for various complex additive+multiplicative sin+cos values across the x-y axis). Basically using this technique I can get 3D-like animations that noone would ever think of, just by twisting knobs, etc. If digital I could also add real 3D space operations to the core vector presentations.

Thus the interest in using a real matrix manipulation stuff (for trigonometry where applicable).

Collapse
 
jackji profile image
jack •

Very nice!

Collapse
 
michalz profile image
Michal Ziulek •

Thanks!

Read next

jackji profile image

A simple async task library

jack -

lhp profile image

Easily create TUI programs with zig-spoon! (project demonstration)

Leon Henrik Plickat -

batiati profile image

IUP for Zig

Rafael Batiati -

kristoff profile image

Struct of Arrays (SoA) in Zig? Easy & in Userland!

Loris Cro -