Introduction
As sports betting expands across the world, more and more players don't understand tha math behind it. So, the purpose of this article it's to clarify how to convert from decimal odds to the probability behind them. The calculations are implemented in Zig, a system programming language perfect to create CLI tools because it's fast and simple.
This article it's divided into two sections: first we'll talk about the math and them about the implementation. If you only need the code you can go directly to my GitHub and this post was originally posted on my blog.
The math
A decimal odd is how much you're going to win for each dollar spent. For example, if the odd is 4.1, for each dollar you bet you're going to receive $4.1. Let's call the decimal odd . The probability related to the decimal odd is
In the example, the probability related to the odd 4.1 is approximate 24.39%.
Let us think the other way now. Given an event with the probability of 20%, let's calculate how much the cassino should pay you:
So, for each dollar spent, the cassino should be paying you 5 dollars, but it doesn't. The cassino only pays you a fraction of it, normally around 95%. The name of this fraction is payout. Naming it Equation 1, let us denote the payout by
and write:
Now calculate the odd with :
Therefore, for each dollar spent, you're going to receive only 4.75 dollars. The 0.25 dollar here is the revenue of the cassino and that's how they can make money with this sorts of gambles.
When the odds are given by the cassino, the payout is unknown and it can vary depending on the time of day, the importance of that game in particular etc. So, we need to calculate first the payout and then we can convert and find the probabilities the cassino is using with Equation 1. Given that the sum of probabilities must be equal to 1 (by the Kolmogorov's axioms), we can write
where N is the number of possible outcomes of the game. For a football game (or soccer for my beloved american readers), the value of N is 3, where all the events are the home team win, the away team win or a draw. For a basketball game, N = 2 (the home team win or the away team win). Since
, the sum of the probabilities can be written as
Isolating , we have now Equation 2:
With the payout calculated we can now use the odds to calculate the probabilities.
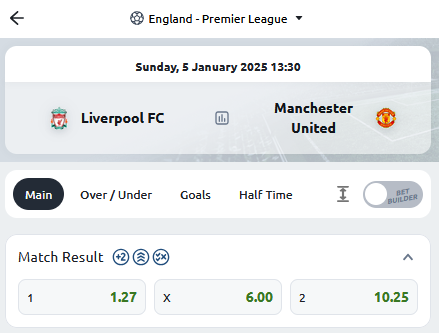
Let's do an example and use the following match odds.
Let
be the probability of Liverpool to win,
the probability of a draw and
be the probability of Man United to win. Calcutating the payout with Equation 2:
With the payout calculated, we can now calculate the probabilities using Equation 1.
-
Liverpool to win:
-
Draw:
-
Man United to win:
Zig implementation
The version of Zig used is 0.13 since it's the last stable release. The implementation must follow three steps:
1) Collect all the odds from the command line;
2) Calculate Equation 2 (payout) and then Equation 1 (the probabilities);
3) Print the values in the screen;
We can start by building an empty project
mkdir zigodd
zig init
To get the arguments from the command line:
const std = @import("std");
const stdout = std.io.getStdOut().writer();
pub fn main() anyerror!void {
const args = try std.process.argsAlloc(std.heap.page_allocator);
defer std.process.argsFree(std.heap.page_allocator, args);
}
A way of implementing the equations above it's creating a struct
that keeps the values of the payout, the odds and the probabilities.
Both of the later starts as empty arrays and the payout start with the value zero.
Two functions are incorporated in the struct: a method for calculating the payout
and other to calculate the probabilities.
const Odds: type = struct {
k: f32 = 0.0,
odds: []f32 = undefined,
probabilities: []f32 = undefined,
pub fn calculate_k(self: *Odds) anyerror!void {
var sum: f32 = 0;
for (self.odds) |item| {
sum += (1 / item);
}
self.k = 1 / sum;
}
pub fn calculate_probabilities(self: *Odds) anyerror!void {
const allocator = std.heap.page_allocator;
var probs_processed = std.ArrayList(f32).init(allocator);
for (self.odds) |item| {
const prob_processed = self.k * (1 / item);
try probs_processed.append(prob_processed);
}
self.probabilities = probs_processed.items;
}
};
Inside the main function, the odds from the arguments can be allocated
in a ArrayList and parsed into a float (f32). To convert to array,
just call the attribute .items.
var myodds = Odds{};
const len_probabilities: u32 = @intCast(args.len);
const odds_raw = args[1..len_probabilities];
const allocator = std.heap.page_allocator;
var odds_processed = std.ArrayList(f32).init(allocator);
defer odds_processed.deinit();
for (odds_raw) |item| {
const odd_processed = try std.fmt.parseFloat(f32, item);
try odds_processed.append(odd_processed);
}
myodds.odds = odds_processed.items;
Also inside the main function, we are now able to call the methods to calculate the values.
try myodds.calculate_k();
try myodds.calculate_probabilities();
Finally, all the values can be printed to the screen.
try stdout.print("-------ZIGODD: ODDS TO PROBABILITY CONVERSOR-------\n", .{});
try stdout.print("---decimal odds to convert: \n", .{});
for (myodds.odds, 0..) |item, index| {
try stdout.print("o{d}: {d:0.2}\n", .{ index + 1, item });
}
try stdout.print("---calculated payout (k): \n", .{});
try stdout.print("k: {d:0.5}\n", .{myodds.k});
try stdout.print("---calculated probabilities: \n", .{});
for (myodds.probabilities, 0..) |item, index| {
try stdout.print("p{d}: {d:0.5}\n", .{ index + 1, item });
}
try stdout.print("-----------------------------------------------------\n", .{});
Note we are not worried about error handling. This should be a real concern to production apps, which is not our case here. As always, the full code is on my [GitHub](https://github.com/vinybrasil/zigodd).
That's it. Fell free to open a PR on the GitHub repo to contact me if you find something wrong. Keep on learning :D
The project can be built with the following code:
zig build
Running the code ./zig-out/bin/zigodd 1.27 6.00 10.25 with the values from the example give us the following result:
-------ZIGODD: ODDS TO PROBABILITY CONVERTER-------
---decimal odds to convert:
o1: 1.27
o2: 6.00
o3: 10.25
---calculated payout (k):
k: 0.9509055
---calculated probabilities:
p1: 0.7487445
p2: 0.1584843
p3: 0.0927713
-----------------------------------------------------
Note we are not worried about error handling. This should be a real concern to production apps, which is not our case here. As always, the full code is on my GitHub.
That's it. Fell free to open a PR on the GitHub repo to contact me if you find something wrong. Keep on learning :D




Top comments (0)